Or will they?

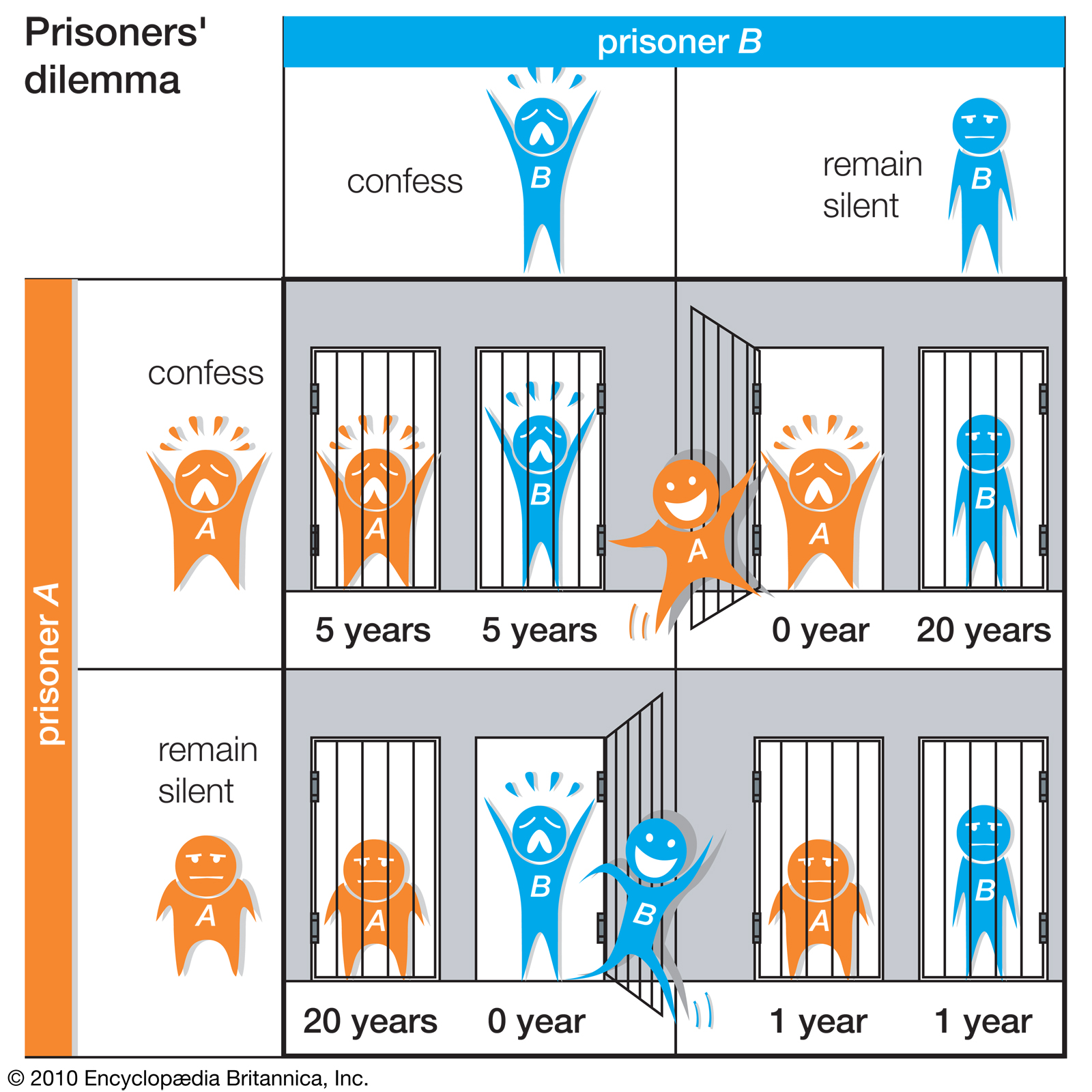
When dealing with cores in game theory, it is easy to know that the best payoffs for each coalition involved can be found in the core. So, does that mean everyone is happy and there’s is nothing else to be discussed? Not even close.

Even once the core is found, there is a matter of finding the best point where everyone is their happiest. There are several methods of going about this including Shapley’s point, finding the nucleous, and the topic of this article: The Gately point. Of the methods that can be used, the Gately point is the most interest to me personally. Instead of looking to provide the highest possible payout or attempting to keep the values as close to one another as possible, this method looks at the player’s temptation to disrupt. The goal of this perspective provides is the keep the gran coalition together. This is done by having the values place that ensures a low temptation to disrupt the coalition.

In the diagram shown above, the formula equates to, ‘how much everyone else will lose, over how much the player in question will lose’. If players are found to be in threat of disrupting then the values are adjusted until a point is reached in which lowering anyone would raise another player.

The Divide the Dollar example is a simple enough premise, three players are given a dollar and told to divide it among themselves. The catch is that it must be decided by majority vote. Under this conditions two of the three players can vote to split the dollar 50-50 and leave the last player with nothing.

The divide the dollar game can be expressed visually through the triangle of imputations. This allows for the players to find the core, in which every coalition formed is doing the best it possibly can. Using this triangle allows for the players to find imputations or a list of payoffs satisfying individual and collective rationality. In this example, the payoffs for each of the players will be X1, X2, and X3. The area of this triangle can be found through the formula A=1/2(s)(h), with s being the sides and h being the height. However, h can be replaced with (X1+X2+X3) as the sum length of each of these lines is equal to the height. These lines can then be used to find fractions which provide how the dollar should be split among the three players. Where the X point is located on the triangle can be changed through bargaining and the formation of coalitions.

The Tragedy of the Commons is an issue of supply and demand, though it’s definition does shift slightly depending on the lens in which it is viewed. A economist may have a very different interpretation of the Tragedy of the Commons than would and environmentalist, philosopher, or even a game theorist. But in it’s most basic form the Tragedy of the Commons can be defined as, a problem in which individuals attempt to gain the greatest benefit from a given resource. Eventually, the demand for the resource increase to a point that the supply can on longer support it, as a result every individual who continues to consume the supply negative effect anyone else who no longer can access the benefits of the resource.

In reality, this issue has been see in a range of place including farming, pollution, and for the example we will be focusing on, international fishing. In the case of the Pacific sardines, which can be caught off the coast of the United States, Canada, and Mexico, a lack of communication between the nations resulted in a failure to manage the rate at which sardines were being caught. This lead to the population to fall due to over fishing as the countries had, thanks to assuming what percentage of the population they had to right to, gone over the amount of fish they were suppose to be catching. If this activity had been left undiscovered the population of sardines would have continued to decrease resulting in negative effects for all three countries. Now, the nations have a tri-national manage agreement to make sure they stay within target levels of fishing.

In terms of Game Theory, the Tragedy of the Commons must be taken into account as in certain scenarios overusing a resource can result loss to payoff. For example, in the cause of farmers sharing a field for their cattle. If each of the six farmers keeps one cow there, they cow will bring in a value of $1000. However, as the number of cattle in the field increase, there are less resources to go around. This results in the value of each cow in the field decreasing by $100, for each addition cow in the field. The farmers must find a way to deal with this issue as to prevent a loss in payoff. In this specific case, a solution can be found in the creation of a coalition, between at least five of the farmers. This sees the farmers working together and agreeing the limit their cattle in the field to only one, as this allows all of them to benefit without activity hurting each others payoffs.

The Prisoners Dilemma is a example that comes up universally throughout majors, minors, and whatever classes a student can hope to find themselves in at most higher level learning institutions. Whether that be philosophy, psychology, economics, general mathematics, or even game theory. For such a widely referenced example, it must be very important and of course, it is agreed upon, right? Well…

The basic break down of the dilemma is as follows, two prisoners have been arrested involved in some from of joint crime. They are told, separately, that if one confesses and the other does not that the one who does will get a payoff while the other will then receive a heavily punishment. In the case that both confess then each will get a lighter sentence, however, if neither confesses then they will both get the lightest sentence. What creates the dilemma is that they are being interrogated separately which means they cannot be sure what their partner is doing. So, what is the best course of action? Do they turn on their partner or do they risk taking the fall for everything?

Unlike many of the games covered over the course of this semester, the Prisoners’ Dilemma comes with an additional dilemma. The best course of action seems to change based on who you ask. Upon talking with my professor, even she seemed to find that other professors that taught the dilemma had different ideas one which is the naive choice versus which is the experienced one. That is not even the only issue that comes into play when discussing this game. Does the optimal strategy change when the game is repeated? Additionally, does it change more depending on how many times it is played?

I chose this game to talk about this week because I felt as it is not often that a game brings up so much discussion on what is the best strategy. Usually, the numbers are able to tell the whole story. However, in this case everything from morality to evolutionary psychology plays a role in what is the best move in a given scenario. Personally, I believe the discussion raised by “The Prisoners’ Dilemma” dilemma is one of the most interesting topics covered so far in game theory.

Game theory focuses not only on player versus player games, but instead goes beyond that to focus on larger events. Some of the situation have been covered previously including the Jamaican fishing example and in the case of war. However, sometimes the real world is not that drastic but you are still faced with a problem. The problem could be something as simple as what you should do on a given day without knowing what the weather could turn out to be. Now, it is possible to simply check ones local new change for the whether, but…whats the fun in that?

Methods:

Laplace: In a given Matrix, select the row option with the highest average entry or highest row sum.

Wald: Take the minimax of the rows, meaning to select the row with the smallest number out of the largest values of each row.

Hurwicz: Involves the use of alpha to signify the coefficient of optimism which will be a value between 0 and 1. Then use the equation,
α(row max) + (1- α)(row min). From there the largest value is selected.

Savage: The values of the matrix are subtracted from the largest number in their column then replaced by the difference. This new matrix is known as a regret matrix and the maximin is taken from the largest values in the new rows.

Why are these important? Each of the given models helps to make decisions when faced against nature. However, they each reveal something different which can help someone make the best choice based on their personal preferences. Each method offers the best of a given criteria. Laplace’s method offers the highest average payoff while Wald’s focuses instead on the certainty that the worst option won’t be awful. It is clear to see the difference in choices someone may make based on whether they are an optimist or a pessimist. This continues with the second two methods, as Hurwicz ensures the possibility for the best of the options. On the other hand, Savage’s method focuses on not having too much regret based on one’s choice. Each method is able to target a specific focus which can better appeal to someone based on their attitude and/or view of the world.

Game Trees are a way for players to make decisions in a sequence based on the choices of the other player. The tree is organized as shown below:

The nodes represent the different players, the branches leading down from the nodes show the choice of the players, and the numbers located at the bottom are the payoffs of the game.

Example: In this example covered in the homework, Colin and Rose are attempting to decide where they are going on a date. Colin gets the choose what they do between the choices of dancing, dinner or movies. Rose then gets the make the choice on the specifics (each listed with the preference of each of the players). In this scenario, Rose has the power because even though Colin gets the make the decision of what they are doing Rose still gets to select the option she wants the most. In this particular movie, the payoff to Rose was 6 as the best choice of Colin was the movies but Rose chose Love Actually. Love Actually’s payout at the bottom of the tree is (6,-4).

Why I liked this game: I found this game to be interesting because it showed how a game can seem fair when in reality one side has a clear advantage. That concept is important moving forward in understanding game theory, even outside the realm of game trees.

Sometimes it is hard to see how Game Theory can be applied outside the classroom, games, and a few very select real world situation such as war. However, an example tackled this week in class focuses on the diverse and real application of game theory.

Game theory was applied to a fishing village in Jamaica during 1960 to compare different areas of fishing when the tide was either running or not. The pots used for fishing could be placed on the inner banks, outer banks, or find a place in between (in-out). While there may be more fish in the outer banks, the rougher seas and unpredictability of the sea offer unique problems such as pots breaking and the need for better boats to minimize risks.

	Current- Running	Current- Not Running
Inside	17.3	11.5
Outer	-4.4	20.6
In-Out	5.2	17

This table shows the average profits in pounds per canoe. After this data was collected to see what the best strategy was for collecting fish and based only on the numbers it showed that outside was the best choice.

Lesson: However, the importance of this example comes from the fact that the real world did not match up with these numbers, as no one was really only using the outside strategy as the risk of losing pots was too great. While there was a benefit to doing so, it was not a large enough benefit to risk losing everything. The people would rather continually gather the same average amount of fish than take the chance to gain more fish while risking it.

Why this Example Matters: I found this example to be the most thought provoking this week because it when to show that outside factors can play a substantial role in human behavior and must be considered just as much as the data. While the numbers tell you how something should play out in a given scenario, that does not guarantee that is exactly how it will happen. This is especially true when it comes to human behavior, which is why this example grabbed my attention as a psychology major.

War is filled with difficult decision making and while the last thing on anyone’s mind while risking their lives for their homes is games, they may want to reconsider that. Game Theory is an integral part of any good strategy, because each side will be looking to take advance of the optimal strategy.

Table:

	A	B	Oddments
A	60	100	40
B	100	80	20
Oddments	40	20

(Left A: unprotected bomber, Left B: protected bomber, Top A: attack on unprotected, and Top B: attack on protected)

Explanation: The table above is from an example entitled The Hidden Object. In this example, there is a military involving two bombers. One bomber contains, unsurprisingly, a bomb while the other has jamming equipment. An enemy jet will get one chance to take down a bomber, but they will only be able to take down one of them. Another fact is that one of the bombers can get protection from the other. These example leads to two questions, which bomber should carry the bomb and which bomber should the enemy fight?

In this example we are given the percent rates of survival for the bombers: 60% for the bomber in the unprotected role, 80% in the protected role, and 100% if not attacked at all.

Now this is where the elements of Game Theory come in. Taking the information from the table we can calculate that the most optimal strategy for the bombers would have the bomb in the protected location 2/3 of the time. On the other side of the coin, it is best for the enemy jet to attack that location 2/3 of the time. How do we get to this conclusion…

Math: The Oddments on the table are found by taking the difference between the values in each of the rows and columns. So, for the first row the difference between 60 and 100 is 40. These numbers are taken and swap, before being put into fractional form. This results in (20/60, 40/60) for both the rows and columns, which when simplified comes out at (1/3, 2/3). These fractions are then plugged into the values of the chart for the protected position as it is the optimal choice. This will give us the value of the game: (1/3)*(60) + (2/3)*(100) = 86.67%, which is the rate of survival given the optimal strategy of placing the carrier with the bomb in the protected position.

I personal found this to be one of the most compelling examples of real world application of Game Theory. While, it is entertaining to figure out how much someone can win in a rigged game, it is a completely different level of understand to see how the information being taught in this course can change the course of something as large as war.

Thanks for joining me!

Good company in a journey makes the way seem shorter. — Izaak Walton